Time-Stepping Optimized for Ocean and Atmosphere Models
We devise and optimize a new class of time-stepping methods tuned specifically for the shallow water equations (SWEs). The SWEs are the foundational equations on which all ocean models are built; our new schemes are between 1.6 and 2.2 times faster (in terms of wall-clock time) than comparable methods.
The new time-stepping scheme presented in this work provides a significant increase to the speed of a shallow water model without sacrificing solution quality. The method can be adapted for use in climate scale ocean models (a version has been recently implemented for single-layer MPAS-Ocean).
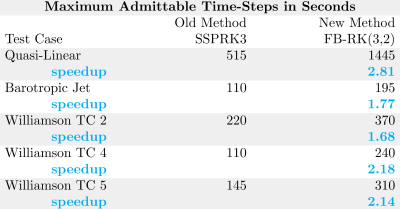
We develop and optimize a class of time-stepping schemes for models relevant to oceanic and atmospheric flows. Specifically for the shallow-water equations, we optimize a schemes that can take time-steps as large as possible while retaining solution quality. These schemes, collectively called FB-RK(3,2), use weighted forward–backward averaging of thickness data to advance the momentum equation. The weights for this averaging are chosen with an optimization process that employs a von Neumann–type analysis, ensuring that the weights maximize the admittable Courant number. FB-RK(3,2) can take time steps up to 2.8 times as large as a popular three-stage, third-order strong stability-preserving Runge–Kutta method in a quasi-linear test case. In fully nonlinear shallow-water test cases relevant to oceanic and atmospheric flows, FB-RK(3,2) outperforms SSPRK3 in admittable time step by factors roughly between 1.6 and 2.2, making the scheme approximately twice as computationally efficient with little to no effect on solution quality.