Resolving the Unresolved: Improving a Statistical Representation of Vertical Structure of Subgrid Clouds
Cumulus towers, those tall storm-forming clouds, and rain shafts are familiar examples of coherent vertical structures in clouds and precipitation, but current models don’t represent them well. This new study found that incorporating more information about the water/ice particles can improve how global climate models represent these structures statistically without having to resolve individual cloud elements.
A more realistic vertical structure of various hydrometeor—airborne cloud water and ice—distributions is needed to accurately model precipitation and radiation processes. This work improves upon current methods and will advance model accuracy.
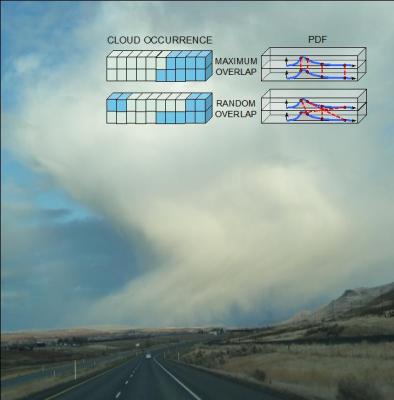
Coarse-resolution climate models increasingly rely on probability density functions (PDFs) to represent an unresolved horizontal variability of clouds and precipitation. A separate treatment, called a PDF overlap assumption, is required to draw representative vertical profiles from these distributions. To model precipitation formation and transfer of solar and thermal radiation in the cloudy atmosphere, these profiles are needed for all hydrometeor (water/ice particle) types predicted by the model. Using detailed numerical simulations which explicitly represent the 3D structure of cloud and precipitation fields, Department of Energy scientists at Pacific Northwest National Laboratory led a team that showed the PDF overlap varies significantly between different hydrometeor types—a distinction not reflected in the current model formulation. Specifically, they found that faster falling raindrops and graupel (soft hail) particles exhibit significantly higher coherence in their vertical distributions than slow falling cloud droplets and ice crystals. The study suggests that to improve the PDF overlap’s representation of vertical structures, the PDF correlations need to depend on the hydrometeor properties, such as fall speeds, in addition to the currently implemented dependency on the convection strength.