Differentiable Modeling to Unify Machine Learning and Physical Models for Geosciences
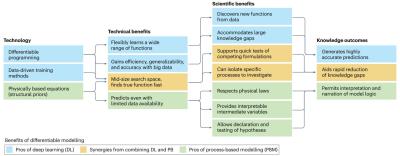
Differentiable modeling involves connecting (flexible amounts of) prior physical knowledge to neural networks, pushing the boundary of physics-informed machine learning. It offers better interpretability, generalizability, and extrapolation capabilities than purely data-driven machine learning, achieving a similar level of accuracy while requiring less training data. Additionally, the performance and efficiency of differentiable models scale well with increasing data volumes. Under data-scarce scenarios, differentiable models have outperformed machine-learning models in producing short-term dynamics and decadal-scale trends owing to the imposed physical constraints.
Knowledge discovery in geosciences can be improved by combining advanced artificial intelligence model architectures with physics using a differentiable programming framework. Although it is often perceived as a technological advance, differentiable modeling can also lead to philosophical changes: for example, it could make it possible to ask new questions, test hypotheses on model structure or data usage, and discover unrecognized physical relationships.
Process-based modeling offers interpretability and physical consistency in many domains of geosciences but struggles to leverage large datasets efficiently. Machine-learning methods, especially deep networks, have strong predictive skills yet are unable to answer specific scientific questions. In this Perspective, we explore differentiable modeling as a pathway to dissolve the perceived barrier between process-based modeling and machine learning in the geosciences and demonstrate its potential with examples from hydrological modeling. ‘Differentiable’ refers to accurately and efficiently calculating gradients with respect to model variables or parameters, enabling the discovery of high-dimensional unknown relationships. Differentiable modeling involves connecting (flexible amounts of) prior physical knowledge to neural networks, pushing the boundary of physics-informed machine learning. It offers better interpretability, generalizability, and extrapolation capabilities than purely data-driven machine learning, achieving a similar level of accuracy while requiring less training data. Additionally, the performance and efficiency of differentiable models scale well with increasing data volumes. Under data-scarce scenarios, differentiable models have outperformed machine-learning models in producing short-term dynamics and decadal-scale trends owing to the imposed physical constraints. Differentiable modeling approaches are primed to enable geoscientists to ask questions, test hypotheses, and discover unrecognized physical relationships. Future work should address computational challenges, reduce uncertainty, and verify the physical significance of outputs.